近日 Apple 發表一篇名為《The Illusion of Thinking(思考的錯覺)》的學術論文,該論文針對多款當前最先進的大型語言模型(LLM),例如Anthropic的Claude 3.7 Sonnet、OpenAI的「o1」與「o3」、DeepSeek的DeepSeek-R1、以及Google的Gemini等,進行了推論能力測試。Apple認為這些大模型的推理表現,遠不如宣傳所言,甚至並沒有在思考(Reasoning)。
Apple AI 團隊研究論文表示:推理模型其實並沒有在「思考」
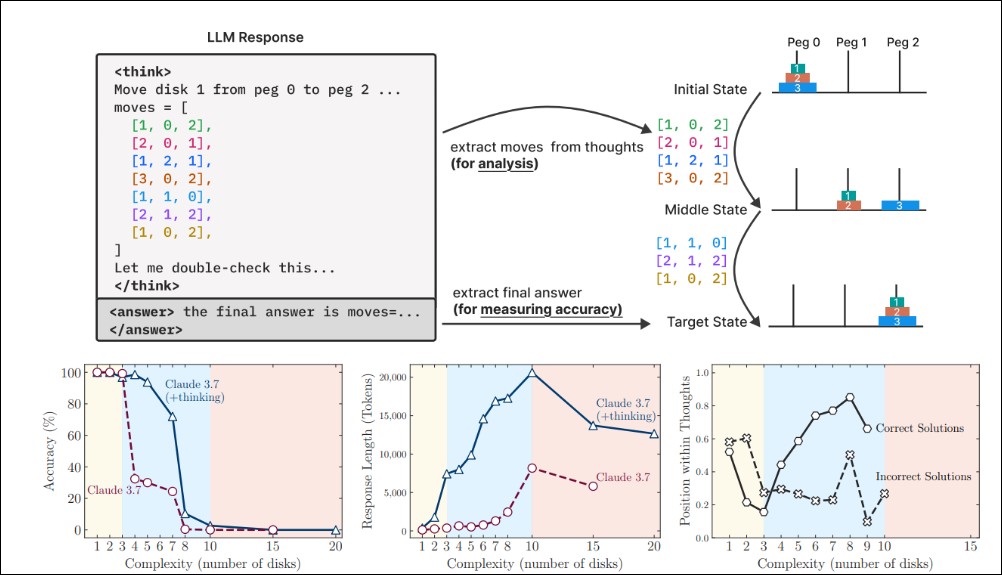
為了瞭解 LRM(大型推理模型)的根本能力、其性能如何隨規模擴展以及潛在局限性,Apple的研究團隊進行了一項系統性的調查,透過可控的解謎環境,精確地操縱問題的組合複雜度,同時保持邏輯結構的一致性,從而揭示LRMs「思考」的真實面貌。透過對LRMs及其對應的標準LLMs在同等推論計算預算下的比較,研究團隊發現了三種截然不同的性能區間,這在傳統數學基準測試中難以觀察到:
-
低複雜度任務區間: 在處理簡單問題時,出人意料的是,標準LLMs展現出更高的效率和準確性,甚至優於LRMs。這表明在某些情況下,額外的「思維」過程可能反而造成冗餘,降低了效率。
-
中等複雜度任務區間: 當問題的複雜度適度增加時,LRMs的優勢開始顯現,其額外的思維過程確實能帶來性能上的提升,與標準LLMs的性能差距也隨之擴大。
-
高複雜度任務區間: 然而,一旦問題的複雜度超越特定閾值,兩種模型——無論是LRMs還是標準LLMs——的性能都會遭遇「徹底崩潰」,準確率趨近於零。這預示著當前推理方法在面對極端複雜問題時,存在根本性的局限。
特別值得注意的是,在接近崩潰點時,LRMs的推理努力(以推論時所消耗的token數量衡量)反而會「反直覺地」下降,即便它們仍有充足的token預算。這意味著LRMs在處理極高複雜度問題時,似乎選擇了「放棄思考」,而非投入更多計算資源以尋求解決方案,這也揭示了其思維能力與問題複雜度之間存在的根本性擴展限制。
為什麼數學基準測試無法充分評估模型能力?
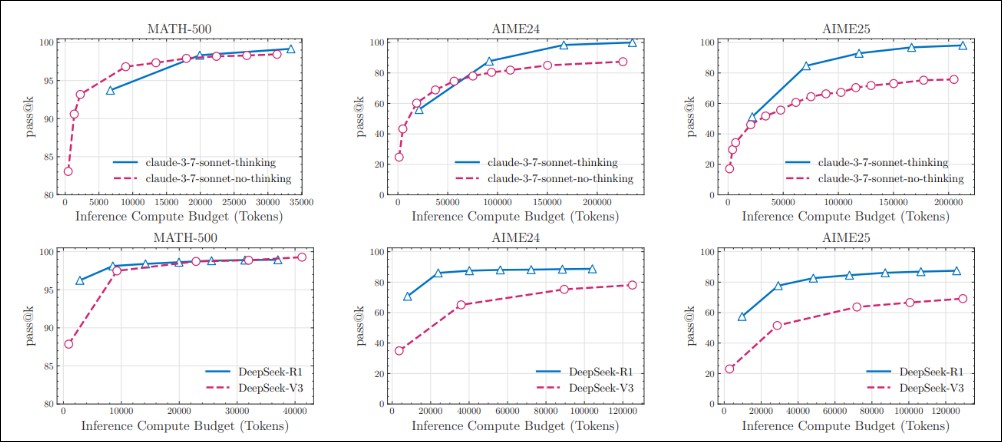
研究指出,當前評估LRMs在既有數學基準測試(如MATH-500、AIME24、AIME25)上的性能增強,究竟應歸因於接觸了更多數學數據、分配了顯著更多的推論計算資源給思維token,還是真正由於其基於強化學習(RL)的訓練而發展出的推理能力,目前尚不明確。
先前的研究和本次實驗結果都證實,在MATH-500數據集上,LRMs的通過率(pass@k)與其非思維型LLMs在相同推論token預算下表現相當。然而,研究團隊觀察到,這種性能差距在AIME24基準測試上有所擴大,並在AIME25上進一步加劇。這種現象帶來了解釋上的挑戰:這可能是因為日益增長的複雜度需要更精密的推理過程,從而凸顯了思維模型在複雜問題上的真正優勢;也可能是因為較新的基準測試(尤其是AIME25)數據污染較少。有趣的是,人類在AIME25上的表現實際上高於AIME24,這暗示AIME25的實際複雜度可能較低。然而,模型在AIME25上的表現卻劣於AIME24,這潛在表明前沿LRMs在訓練過程中可能存在數據污染。
鑑於這些難以解釋的觀察結果,以及數學基準測試無法實現對問題複雜度的精確控制,研究團隊轉向了可控的「解謎環境」進行更精確和系統化的實驗。
可控解謎環境:揭示「思考」的真相
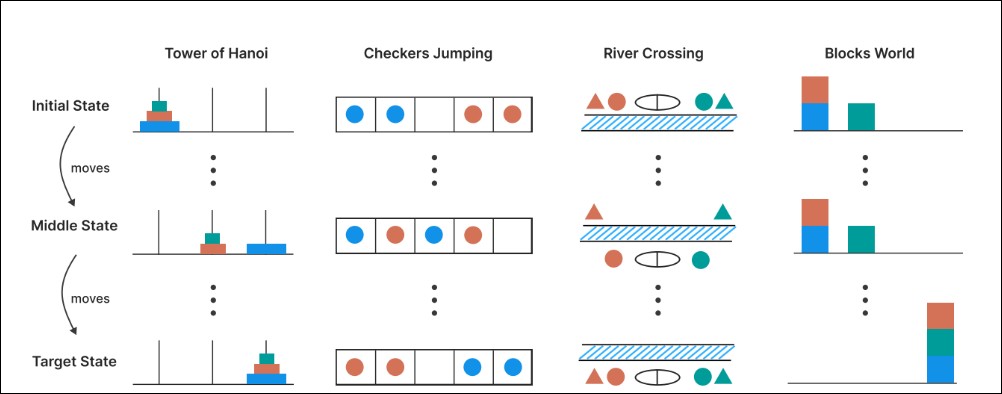
為了更嚴謹地理解LRMs的推理行為,研究團隊採用了四種可控的解謎環境進行實驗:
-
河內塔 (Tower of Hanoi): 經典的遞迴謎題,透過調整碟片數量控制複雜度。
-
跳棋 (Checkers Jumping): 一維排列的跳棋遊戲,透過調整棋子數量控制複雜度。
-
渡河問題 (River Crossing): 一種約束滿足規劃謎題,透過調整參與者對數控制複雜度。
-
積木世界 (Blocks World): 積木堆疊謎題,透過調整積木數量控制複雜度。
這些謎題環境具有以下關鍵優勢:
-
精細控制複雜度: 允許研究人員透過調整謎題元素(如碟片、棋子、積木或參與者數量)來系統地改變問題複雜度,同時保持核心邏輯不變。
-
避免數據污染: 不同於既有基準測試,這些謎題設計旨在避免數據污染,確保模型必須依賴真正的推理能力而非記憶。
-
強調演算法推理: 謎題僅需明確提供的規則,強調演算法推理,而非過度依賴廣泛的知識。
-
支援模擬器評估: 能夠進行嚴格、基於模擬器的評估,實現對解決方案的精確檢查和詳細的失敗分析。
透過這些環境,研究團隊不僅能評估最終答案,還能深入分析模型內部生成的「思維痕跡」(reasoning traces),即模型在得出答案前的詳細思考過程。
推理模型的「崩潰」模式與思維動態
實驗結果明確指出,所有接受評估的LRMs(包括03-mini、DeepSeek-R1、DeepSeek-R1-Qwen-32B和Claude-3.7-Sonnet-thinking)都表現出相似的模式:隨著問題複雜度的增加,準確率逐漸下降,最終在超越模型特定的複雜度閾值後徹底崩潰(準確率為零)。奇妙的是,在接近準確率崩潰點時,LRMs所分配的思維token數量:也就是它們的推理努力會反直覺地減少。即使在仍有充足推論預算的情況下,這些模型也未能利用額外的計算資源來進行更深入的思考。這種行為強烈暗示了當前推理模型在思維能力上存在著與問題複雜度相關的根本性擴展限制。
透過對Claude-3.7-Sonnet-Thinking模型在不同謎題中的思維痕跡進行精細分析,研究團隊進一步揭示了模型「思維」過程中的複雜模式:
-
低複雜度下的「過度思考」: 對於簡單問題,模型往往在思維過程的早期就找到了正確的解決方案,但隨後卻繼續探索不正確的替代方案,導致計算資源的浪費。不正確解決方案的分佈在思維過程的後期更為集中。
-
中等複雜度下的先錯後對: 隨著問題複雜度的適度增加,這種趨勢發生逆轉:模型傾向於首先探索不正確的解決方案,而在思維過程的後期才逐漸找到正確的解決方案。此時,不正確解決方案的分佈更為靠前。
-
高複雜度下的徹底錯誤: 對於高複雜度問題,模型完全無法在思維過程中產生任何正確的解決方案,陷入徹底崩潰。
這項分析也顯示,對於較簡單的問題,解決方案的準確性會隨著思考的進行而下降或波動,這進一步印證了「過度思考」現象的存在。然而,對於更複雜的問題,解決方案的準確性會隨著思考的進行而提高,直到達到某個閾值。超越這個閾值,即進入「崩潰模式」後,準確率則降為零。這表明LRMs的自我修正能力雖然有其價值,但也存在根本性的效率低下和明顯的擴展局限性。
研究還揭示了LRMs在執行精確問題解決步驟方面的局限性:
-
提供演算法卻無助於性能: 即使直接在提示中提供了解決河內塔問題的明確演算法,模型在執行這些既定步驟時的性能也並未顯著提高,崩潰點大致保持不變。這令人費解,因為找到並設計解決方案理應比單純執行給定演算法需要更多的計算量。這進一步突顯了推理模型在驗證和遵循邏輯步驟解決問題方面的局限性。
-
謎題間的表現不一致性: Claude 3.7 Sonnet Thinking模型在不同謎題之間展現出極為不同的行為。在河內塔問題中,即使N=10,模型在解決方案中首次出現錯誤也通常發生在較晚的步驟(例如第100步左右)。然而,在渡河問題中,模型卻僅能產生最多4個有效步驟就宣告失敗。值得注意的是,模型能夠以近乎完美的準確率解決需要31步的N=5河內塔問題,卻無法解決僅需11步的N=3渡河問題。這可能表明在網路數據中,N>2的渡河問題實例極為稀缺,導致LRMs在訓練期間未能頻繁遇到或記憶這些案例。
總結
蘋果AI團隊的論文透過設計可控的謎題環境,系統性地揭示了LRM在處理不同複雜度問題時的真實表現,並對其「思考」的本質提出了深刻的質疑。
論文的主要發現可以總結為以下幾點:
- 泛化能力受限:LRM在特定複雜度閾值後,解決問題的準確性會完全崩潰,表明其泛化能力遠不如預期。
- 推理努力的非線性縮放:模型的推理努力(token使用量)並非隨著問題複雜度無限增加,反而會出現反常的下降趨勢,揭示了其推理能力的根本性縮放限制。
- 性能區間差異:在低複雜度任務上,標準LLM可能表現更優;在中等複雜度上,LRM展現優勢;但在高複雜度下,兩者均會失效。
- 「過度思考」現象:LRM在簡單問題上會出現冗餘的推理過程,效率低下。缺乏精確計算與推理不一致:模型未能有效利用顯式演算法,且在不同謎題類型上表現出推理不一致性。
這些發現共同指向一個結論:儘管LRM能夠生成看似合理的推理過程,但這更多是基於對訓練數據中模式的統計學習和重現,而非真正意義上的邏輯推理和問題理解。它們的「思考」是一種表象,一種「幻象」,其本質仍是複雜的模式匹配,而非人類所具備的通用、可泛化的智慧。
這項研究對未來人工智慧的發展具有重要的意義,未來 AI 的研究方向應更加注重以下幾個方面:
- 提升泛化能力:開發能夠將所學知識和推理策略有效泛化到未見過問題和更高複雜度場景的模型。
- 優化推理效率:解決「過度思考」等效率問題,使模型能夠更高效、更精準地利用計算資源進行推理。
- 增強演算法理解:探索如何賦予模型真正的演算法理解能力,使其能夠像人類一樣,透過明確的邏輯規則來解決問題,而非僅僅依賴模式匹配。
- 建立更嚴謹的評估體系:設計更多可控、透明且能夠深入分析模型內部推理過程的評估基準,以更準確地衡量AI的真實能力。
不過不知道蘋果 AI 至今還沒有拿出讓人驚艷 AI 應用,是不是也是因為這些原因才導致進展緩慢呢?